Yb Hollow Cathode Lamp absorption spectrum
Part I of the UMD Physics Quantum Information Group Rotation course (Spring 2009)
Abstract:
A measurement of the absorption spectrum of the Ytterbium (Yb) present in a hollow cathode tube was done with the use of a 399 nm diode laser. The beam passed through a region near the cathode which sputters Yb atoms. The light was then collected by a detector and the output measured as a DC voltage on an oscilloscope after low-pass filtering and amplifying the signal using a Low-noise preamplifier. Based on the absorption spectrum, we were able to estimate the Yb atom density.
Introduction:
Lasers exhibit frequency drifts as a consequence of temperature variation, lasing medium impurities, vibrations, electronic noise, etc. The use of lasers for research in quantum/atom optics demands high control of the frequency. Therefore, the presence of drifts are a nuisance, and stabilization or locking techniques have been developed. One such technique, consists of finding a suitable element whose transitions lie very close to the laser wavelength which is wished to be locked. A cell can be built containing the element (Examples are: I2, Rb and Yb). The absorption spectrum obtained after shining the laser through the cell, although broader than the laser linewidth, provides a more accurate reference for the frequency that is desired. At this point a laser scan is carried out and compared to the absorption spectrum which yields an error signal that is feedback into the laser to perform the necessary adjustments.
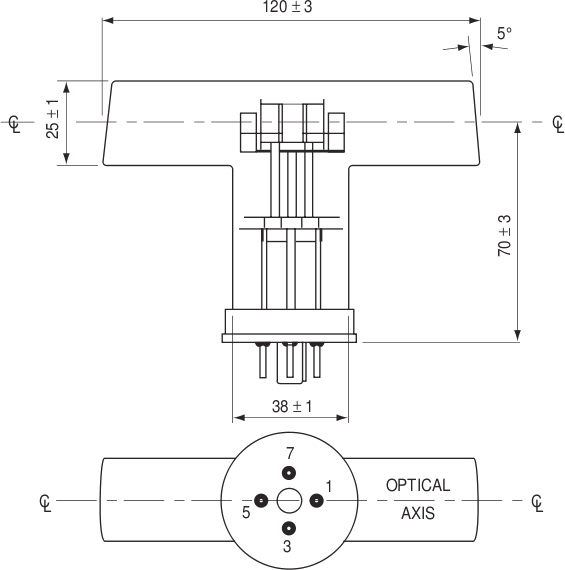
For a 399 nm laser, Ytterbium has a dipole-allowed (E1) transition between levels (6s 6p)1P1 and (6s2)1S0 which makes it an ideal candidate as can be evidenced from fig. 1. Even though it is common practice to use a vapor cell for other elements, Yb is not quite so easy. Nevertheless, it has been shown [1], that a hollow cathode lamp (HCL) can achieve good results. These lamps roughly consist of a cathode made of the element in question and an anode located closely on top (see fig. 2), usually ring shaped, all enclosed in a special glass (UV glass or borosilicate)
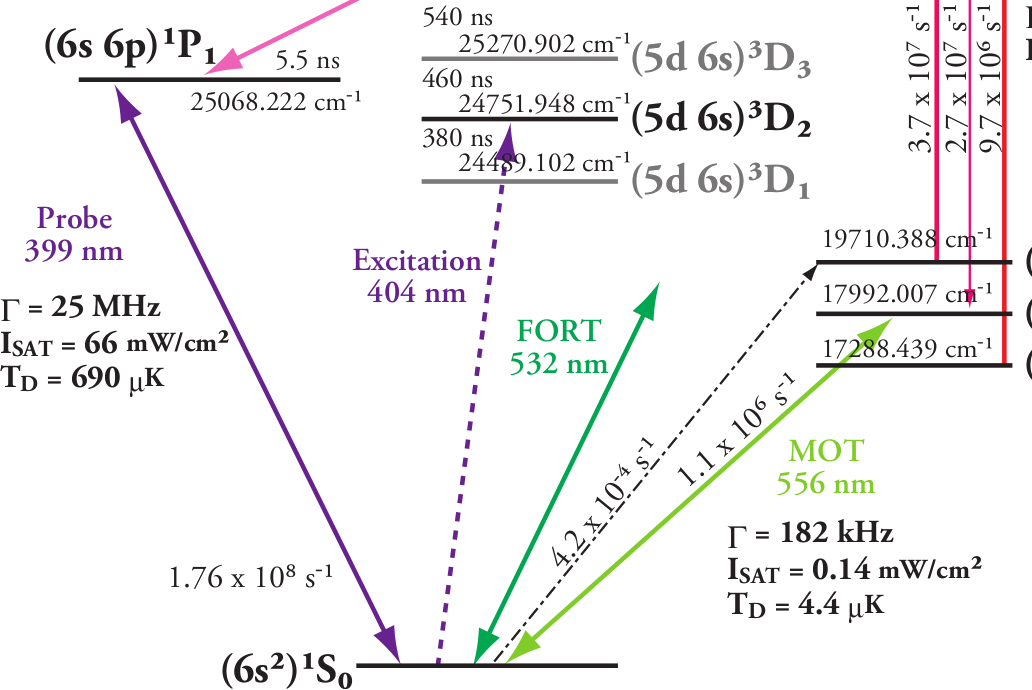
|

|
| Fig. 1. Neutral Yb energy diagram of interest | Fig. 2. Yb Hollow Cathode Lamp example |
Experiment:
For the experiment, a 5UN/Yb Ytterbium Hollow Cathode Lamp was used. It was manufactured by Cathodeon for use in Fisher Scientific spectrometers. Its cathode if made of Yb and has a ring shaped anode. It also contains Neon as fill gas. Its specifications are as follows:
| Diameter | 50 mm |
|---|---|
| Striking Voltage | 180 V |
| Running Voltage | 165 V |
| Current | 30 mA |
| Cathode | Pin B |
| Anode | Pin A |
The 399 nm laser brought to my working space via an optical fiber passed through a region near the cathode which is actively sputtering Yb atoms (see fig. 4), and has a presumably higher atom density than other regions of the lamp. Upong exiting the lamp, the beam encountered two irises before reaching the detector. These irises and the black tape with which the lamp was covered were designed to block any background and lamp light also reaching the detector. The setup can be seen on fig. 3.

|
|
| Fig. 3. Optical bench setup | Fig. 4. Beam path through the Yb HCL |
The detector was kept at a gain of 40 dB. But even so, the signal measured as a DC voltage across the detector using an oscilloscope was very weak (with the lamp on or off). Thus we used a Low-noise preamplifier to boost the signal using a gain of 2 x 102 and also applying a low-pass filter to get rid of unwanted signals with frequencies higher then 30 Hz. The output was then connected to the oscilloscope.
Initially, a laser scan was going to be done. Unfortunately, the 399 nm laser had problems because it was operating in multiple modes. Thus, only the absorption spectrum was determined. This was done, by varying the laser wavelength about 1 GHz off resonance (with the Yb atoms) and measuring the DC voltages in the oscilloscope with only the laser on and with both the laser and the lamp on. Additionally the background was measured (laser and lamp off) and the output solely due to the lamp (see fig. 5).
Results:
It is known that the spectrum of an atomic transition does not resemble a dirac delta function, but rather a broad distribution. There are many factors that cause broadening. There are two main cathegories, homogeneous and inhomogeneous [2]. The most important type of homogeneous broadening that concerns us is the so-called natural broadening. This natural broadening for the transition in study for neutral Yb is 25 Mhz, as can be seen on fig. 1.
However, the most important contribution to the broadening of our spectrum, will undoubtedly come from the most important type of inhomogenous brodening, called doppler. Using the following equation [2] :
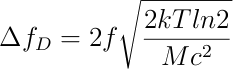
We plotted the doppler broadening as a function of temperature, since this was the only parameter unknown to us. Thus we obtained:
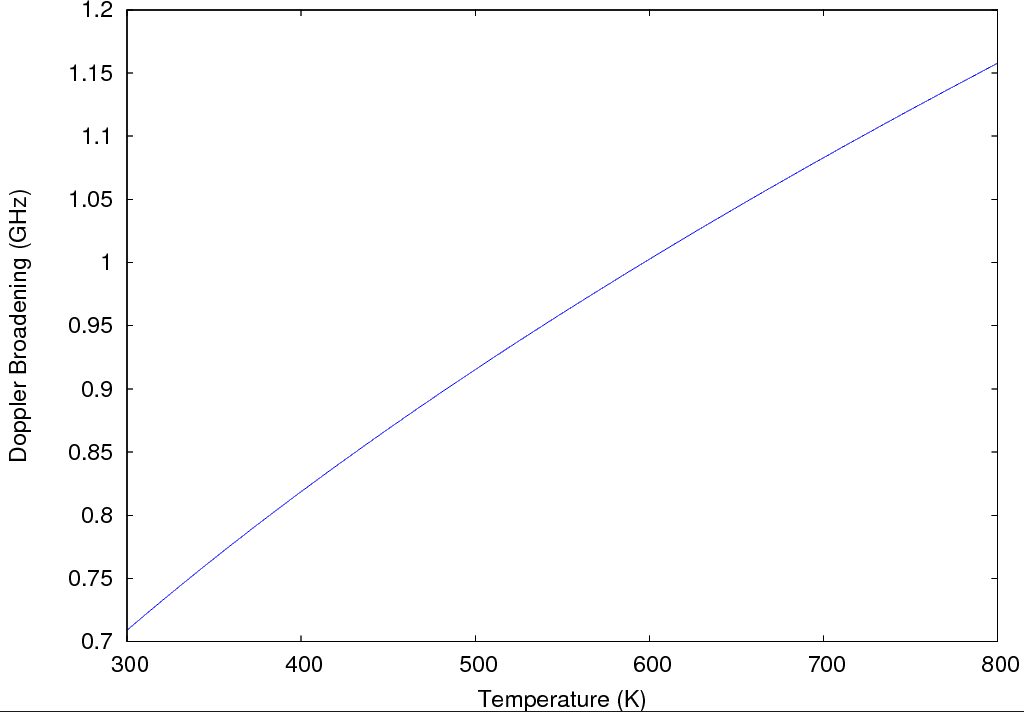
Fig. 6. Doppler broadening as a function of temperature
We therefore assumed the doppler broadening to be of the order of 1 GHz, meaning this is the order of magnitude of the variation needed in the laser frequency to probe the absorption of the Yb atoms present in the hollow cathode tube. After measuring the voltages for the cases mentioned above and plotting the appropriate percent difference we obtain the absorption spectrum for the Yb lamp:
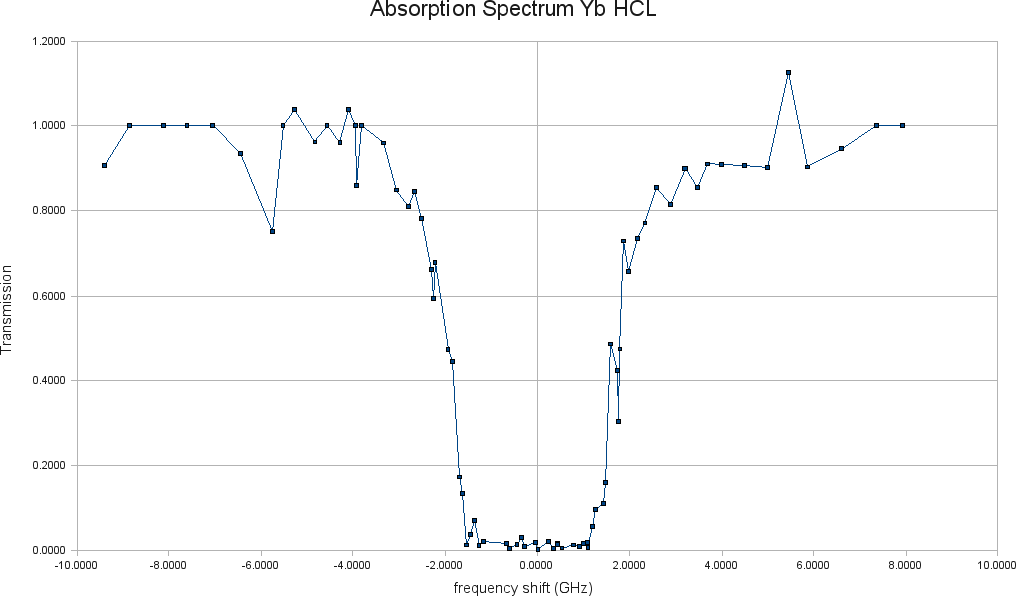
Fig. 7. Yb HCL absorption spectrum
Using now the value of the smallest transmission obtained from the spectrum (T = 0.0021) at resonant frequency (&lambda = 398.91108 nm), we can estimate the atom density present in the region of the HCL through which the laser beam is passing through. This is done using the well-known Beer-Lambert law [3] :
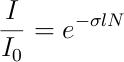
Where l is the distance traversed by the beam in the medium and is equal to the diameter of the lamp (l = 5.0 cm), N is the atom density and &sigma is the absorption cross section. Thus, we need to estimate the cross section to be able to calculate the density. The absorption cross section can be calculated as follows [4] :
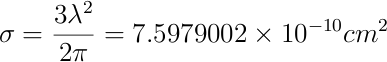
Now, using this number, we can find N :
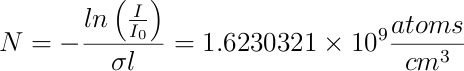
Discussion and Conclusions:
The results obtained here are, of course, only preliminary. In order to fully understand if this Yb HCL will serve to lock to 399 nm, a laser scan must be done. However, the absorption spectrum clearly indicates its potential. Achieving almost zero transmission is proof of this.
The spectrum did not have a width of 1 GHz as we had expected. This was due to two factors. For one, the Yb gas present is composed of several isotopes, each one of which has a slightly different resonant frequency, causing several distributions to overlap. Also, according to [1], homogeneous pressure broadening is also contributing (this is due, mostly to collisions between the atoms present in the gas).
To calculate the atom density I used the diameter of the lamp as the distance traveled by the beam. Though this is likely a good approximation, it is clear the number of Yb atoms will be negligible relatively close to the cathode. Perhaps using the diameter of the cathode would be a better estimate and could potentially cause an increase in the value calculated for the density up 1 order of magnitude
Acknowledgements
I would like to thank Dr. Wes Campbell for all his help and guidance in the lab, Prof. Chris Monroe for suggesting the project and his help and Prof. Luis Orozco for the opportunity to take this course.
References:
- arXiv:0806.1794v1 [physics.optics].
- C. C. Davis, Lasers and electro-optics: fundamentals and engineering (Cambridge University Press, 1996).
- Wikipedia contributors, Beer-Lambert law, Wikipedia, the free encyclopedia (2008, February). Retrieved April 1, 2009, from http://en.wikipedia.org/wiki/Beer-Lambert_law
- H. J. Metcalf and P. van der Straten, Laser Cooling and Trapping (Springer, New York, 1999).



